Criterios de divisibilidad
¡Buenos días!
Tal y como vimos en clase, estamos con el tema de los criterios de divisibilidad.
En primer lugar, recordad que un criterio de divisibilidad es una forma que tenemos que comprobar si un número es divisor de otro o no. Es decir, los utilizamos para saber si, por ejemplo 1234 es divisible por 2, 1505 por 5 o 12121212 por 3.
Para poder decir que un número es divisible por otro, es necesario que la división sea exacta. Por ejemplo, 15 es divisible por 3, ya que 15:3= 5; su resto es 0.
Para poder decir que un número es divisible por otro, es necesario que la división sea exacta. Por ejemplo, 15 es divisible por 3, ya que 15:3= 5; su resto es 0.
"Pero es fácil... divido y ya está". Sí y no. Por un lado, tienes toda la razón: si inviertes tiempo dividiendo, lograrás un resultado que te dirá si es divisible o no. Por otro, puedes ganar tiempo sin hacer la división aplicando los criterios de divisibilidad.
Aquí os dejo una tabla que resume los que hemos trabajado en clase.
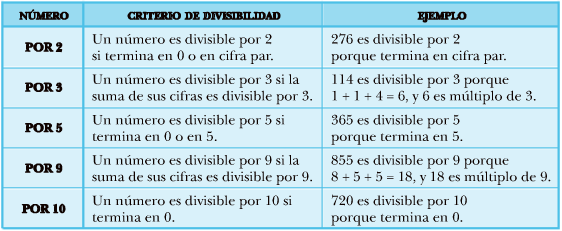 |
| Incorporado de Clase C en marcha |
Si lo que os estáis preguntando es "¿hay más criterios de divisibilidad?", mi respuesta es: ¡y tanto que sí!
Os incluyo también los del 6 y los del 4, que pueden ser un poco más complejos al principio, pero que estoy seguro que podréis aprender.
 |
| Imagen tomada de Maestro San Blas Este vídeo explica cómo obtener todos los divisores de un número y cuáles son los criterios de divisibilidad. Para practicar, os dejo varias actividades interactivas (la del vídeo haciendo click aquí y otra que os presento abajo). ¡Mucho ánimo! |


Una pregunta: En la foto que tomaste de maestro San Blas pone que un número es divisible por nueve di la suma de sus cifras da finalmente nueve. Yo creo que eso no es correcto si no que lo correcto es que es divisible si sus cifras al sumarlas de un múltiplo del nueve.¿Cuál de las dos es correcta?
ResponderEliminarYo creo que las dos son correctas. Si sigues sumando las cifras acaban sumando 9
ResponderEliminarPor ejemplo el número 57222 es múltiplo de 9 , sus cifras suman 18, múltiplo de 9.pero si sigues sumando las cifras 18/ 1+8 =9....finalmente da siempre 9